 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Делимость-2 >> Малая теорема Ферма | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Делимость-2. Малая теорема Ферма |
|
|
Пусть ka ≡ kb (mod %)%m, k и m – взаимно просты. Тогда a ≡ b (mod %)%m.
Задача 86:
Пусть ka ≡ kb (mod kn). Тогда a ≡ b (mod %)%n.
Задача 87:
Найдите остаток от деления 2¹ºº на 101.
Задача 88:
Найдите остаток от деления 3¹º² на 101.
Задача 89:
Докажите, что 300³ººº – 1 делится на 1001.
Задача 90:Найдите остаток от деления 8900 на 29.
Задача 91:
Докажите, что 7¹²º – 1 делится на 143.
Задача 92:
Докажите, что число 30239 + 239³º – составное.
Задача 93:
Пусть p – простое число. Докажите, что (a + b)p = ap + bp (mod %)%p для любых целых a и b.
Задача 94:
Сумма трех чисел a, b и c делится на 30. Докажите, что a5 + b5 + c5 также делится на 30.
Задача 95:
Пусть p и q – различные простые числа. Докажите, что
а) pq + qp = p + q (mod pq).
б) 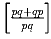 – четное число, если p,
q ≠ 2.
– четное число, если p,
q ≠ 2.
Задача 96:
Пусть p – простое число, и a не делится на p. Докажите, что найдется натуральное число b, для которого ab ≡ 1 (mod p).
Задача 97:
(Теорема Вильсона). Пусть p – простое число. Докажите, что (p – 1)! ≡ – 1 (mod %)%p.
Задача 98:
Пусть n – натуральное число, не кратное 17. Докажите, что либо n8 + 1, либо n8 – 1 делится на 17.
Задача 99:
а) Пусть p – простое число, отличное от 3. Докажите, что число 111 … 11 (p единиц) не делится на p.
б) Пусть p > 5 – простое число. Докажите, что число 111 … 11 (p – 1 единица) делится на p.
Задача 100:
Докажите, что для любого простого p разность 111 … 11222 … 22333 … 33 … 888 … 88999 … 99 – 123456789 (в первом числе каждая ненулевая цифра написана p раз) делится на p.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Делимость-2 >> Малая теорема Ферма | Показать решения |