 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Геометрия >> Площадь | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Геометрия. Площадь |
|
|
Длины сторон выпуклого четырехугольника равны a, b, c и d (перечислены по часовой стрелке). Докажите, что площадь четырехугольника не превосходит а) (ab + cd)/2; б) (a + b)(c + d)/4.
Задача 41:
Могут ли длины высот треугольника относиться друг к другу как 1:2:3?
Задача 42:
Треугольник площади 1 имеет стороны с длинами a,
b и c, причем a ≥ b ≥ c. Докажите, что 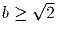 .
.
Задача 43:
Могут ли длины всех сторон треугольника площади 1 быть больше 1000?
Задача 44:
Точки K, L, M и N – середины сторон выпуклого четырехугольника ABCD. Докажите, что 2S(KLMN) = S(ABCD).
Задача 45:
Найдите площадь выпуклого четырехугольника ABCD, если прямая AC перпендикулярна прямой BD и AC = 3, BD = 8.
Задача 46:
Дан треугольник ABC. Точка A1 лежит на продолжении стороны BC за точку C, причем BC = CA1. Аналогично строятся точки B1 и C1. Найдите S(A1B1C1), если S(ABC) = 1.
Задача 47:
Точка M лежит внутри треугольника ABC. Докажите, что площади треугольников ABM и BCM тогда и только тогда, когда M лежит на медиане BK.
Задача 48:
Если два выпуклых четырехугольника расположены так, что середины сторон у них совпадают, то их площади равны. Докажите это.
Задача 49:
Диагонали трапеции ABCD (BC || AD) пересекаются в точке O. Докажите, что треугольники AOB и COD равновелики.
Задача 50:
Докажите, что сумма расстояний от точки, находящейся внутри правильного треугольника, до его сторон не зависит от положения точки.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Геометрия >> Площадь | Показать решения |