 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Индукция в неравенствах | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Неравенства. Индукция в неравенствах |
|
|
Докажите, что при n ≥ 3 выполняется неравенство
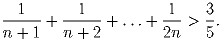
Задача 53:
n – натуральное число. Докажите, что
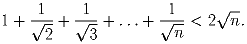
Задача 54:
n – натуральное число. Докажите, что
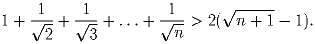
(54) Решение совершенно аналогично предыдущему. Нужно лишь поменять знаки неравенств.
Задача 55:
n – натуральное число. Докажите, что
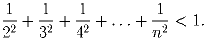
(Неравенство Бернулли). x ≥ 0, n – натуральное число. Докажите, что (1 + x)n ≥ 1 + nx.
Задача 57:
n – натуральное число. Докажите, что nn > (n + 1)n – 1.
Задача 58:
n – натуральное число, n ≥ 4. Докажите, что n! ≥ 2n.
Задача 59:
n – натуральное число. Докажите, что 2n ≥ 2n.
Задача 60:
При каких натуральных n выполняется неравенство 2n ≥ n³?
Задача 61:
Докажите, что для любого натурального n выполняется неравенство 3n > n • 2n.
Задача 62:
Какое из чисел
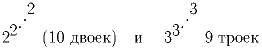
Задача 63:
Произведение положительных чисел a1, a2, …, an равно 1. Докажите, что (1 + a1)(1 + a2) … (1 + an) ≥ 2n. Замечание. У задачи 63 имеются и другие решения, помимо индуктивного.
Задача 64:
Докажите неравенство Бернулли (1 + x)n ≥ 1 + nx, если известно лишь, что x ≥ – 1 и n ≥ 1.
Задача 65:
Сумма положительных чисел x1, x2, …, xn равна 1/2. Докажите, что
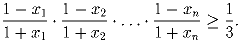
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Индукция в неравенствах | Показать решения |