 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Заключительная олимпиада | Показать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2000 г, 6 класс. Заключительная олимпиада |
|
|
Юра задумал число, умножил его на 13 и зачеркнул последнюю цифру результата. Полученное число Владик умножил на 7, вновь зачеркнул последнюю цифру результата и получил 21. Каким могло быть задуманное число? Не забудьте привести все возможные варианты.
Задача 2:В некоторой компании все, кроме одного, родились в 1988 году или в июне, все, кроме одного, – в 1989 году или в июле, и все, кроме одного, – в 1990 году или в августе. Сколько человек в этой компании?
Задача 3:
Фигуру, изображённую на рисунке, разрежьте на две части
так, чтобы из них можно было сложить прямоугольник.

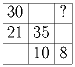
Прямоугольник разделён двумя вертикальными и двумя горизонтальными разрезами на девять прямоугольных частей. Площади некоторых из них указаны на рисунке. Найдите площадь верхней правой части. Ответ обоснуйте.
50 детей водят хоровод, держась за руки. Докажите, что найдутся хотя бы два ребёнка, каждый из которых держит за руки либо двух мальчиков, либо двух девочек.
Задача 6:
На девяти карточках написаны числа от 1 до 9. Два игрока по очереди берут по одной карточке. Выигрывает тот, кто первым сможет составить с помощью своих карточек, знаков « + », « – ", « × ", «:" и скобок арифметическое выражение, значение которого равно 50. Составлять из карточек многозначные числа не допускается. Кто выигрывает при правильной игре и как ему следует играть?
Задача 7:a, b, c – нечётные натуральные числа, не являющиеся квадратами. Может ли число ab • bc • ca быть полным квадратом?
Задача 8:90 яблок разложены по нескольким ящикам. Докажите, что можно съесть часть яблок так, чтобы во всех непустых ящиках осталось поровну яблок, а общее число оставшихся яблок было не менее 20.
Задача 9:
Константин Александрович выписал на доске 6930 единиц. Вначале он изменил знак у каждого 5-го числа, затем – у каждого 7-го, после этого – у каждого 9-го, и, наконец, у каждого 22-го. А теперь он спрашивает вас: какова сумма чисел, записанных на доске?
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Заключительная олимпиада | Показать решения |