 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Формула Пика | Показать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Формула Пика |
|
|
Задача 2: Теорема. Вершины многоугольника (не обязательно выпуклого) расположены в узлах клетчатой бумаги. Внутри него лежит n узлов, а на границе m узлов. Докажите, что площадь этого многоугольника равна n + m/2 – 1 (Формула Пика).
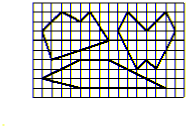
Задача 3: Убедитесь в справедливости формулы Пика для многоугольников, изображенных на рисунке 1. Задача 4: Докажите формулу Пика, разбив доказательство на ряд шагов:
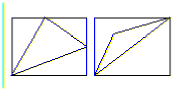
б) Вершины треугольника расположены в узлах клетчатой бумаги, причем на его сторонах других узлов нет, а внутри есть ровно один узел O. Докажите, что O – точка пересечения медиан треугольника.
Задача 9: Пусть A и B два узла клетчатой бумаги, из которых, второй на p клеток правее и на q клеток выше первого. Чему равно расстояние от прямой AB до ближайшего к ней узла, не лежащего на этой прямой? Задача 10: Докажите, что найдется прямая, проходящая через два узла клетчатой бумаги, и не лежащий на этой прямой узел, такой, что расстояние между ними меньше 1/2000. Задача 11: а) Докажите, что для любого многоугольника с вершинами в узлах сетки отношение его площади к квадрату любой стороны рационально.б) Найдется ли правильный треугольник с вершинами в узлах сетки?
Задача 12: Шахматный король обошел доску 8 × 8 клеток, побывав на каждом поле ровно 1 раз и последним ходом вернувшись на исходное поле. Ломаная, последовательно соединяющая центры полей, не имеет самопересечений. а) Нарисуйте такую ломаную; б) найдите площадь, ограниченную этой ломаной. Задача 13: Докажите, что если вершины выпуклого n-угольника лежат в узлах клетчатой бумаги, а внутри и на его сторонах других узлов нет, то n < 5. Задача 14: Найдется ли прямоугольный треугольник с целыми сторонами и вершинами в узлах сетки а) на сторонах которого нет узлов сетки кроме вершин; б) ни одна из сторон которого не проходит по линиям сетки? Задача 15: На большой шахматной доске отметили 2n клеток так, что ладья может ходить по всем отмеченным клеткам, не перепрыгивая через неотмеченные. Докажите, что фигуру из отмеченных клеток можно разрезать на n прямоугольников. Задача 16: Ладья, шагая по одной клетке, за 64 хода обошла все клетки шахматной доски и вернулась на исходную клетку. Докажите, что число ходов по вертикали не равно числу ходов по горизонтали.| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Формула Пика | Показать решения |