 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Геометрические неравенства-2 | Показать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Геометрические неравенства-2 |
|
|
б) А где нужно строить автобусную остановку, если деревни расположены по одну сторону от шоссе?
Задача 4:
Серый Волк хочет оживить Ивана-Царевича. Как ему добраться до Ивана кратчайшим путем, набрав по дороге мертвой и живой воды (см. рис.)?
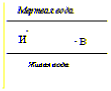
Задача 5:
Точка M лежит внутри острого угла AOB. Найдите на сторонах угла такие точки N и P, что треугольник MNP имеет наименьший возможный периметр.
Задача 6: Докажите, что если отрезок, соединяющий середины сторон четырехугольника, равен полусумме двух других его сторон, то две эти другие стороны параллельны.
Задача 7: Среди всех треугольников с данными сторонами AB и AC найдите тот, у которого наибольшая площадь. Задача 8: На биссектрисе внешнего угла C треугольника ABC взята точка M, отличная от C. Докажите, что MA + MB > CA + CB.
Задача 9:
Петя хочет пройти к киоску на другом углу перекрестка (см. рис.). Каждую дорогу (полосу с параллельными краями) он должен пересечь под прямым углом. Постройте для него кратчайший путь.
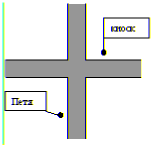
Задача 11:
Внутри угла лежат две точки A и D. Соедините их ломаной ABCD наименьшей длины с точками B и C на разных сторонах угла.
Задача 12:На плоскости дано n красных и n синих точек, никакие три из которых не лежат на одной прямой. Докажите, что можно провести n отрезков с разноцветными концами, не имеющих общих точек.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Геометрические неравенства-2 | Показать решения |