Задача 1:
Из квадрата клетчатой бумаги размером 2
n × 2
n вырезали одну
угловую клетку. Докажите, что полученную фигуру можно разрезать на
«уголки» из трех клеток.
Задача 2:
Последовательность
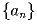
задана правилом:
a
1 = 1, а каждый член, начиная со второго, вычисляется
по формуле a
n + 1 = 2a
n + 1. Докажите, что a
n = 2
n – 1.
Задача 3:
Докажите, что любую сумму, начиная с 8 рублей, можно выплатить монетами по 3
рубля и 5 рублей.
Задача 4:
Доказать тождества:
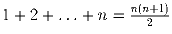 ;
;- 1 + 3 + … + (2n – 1) = n²;
 ;
; ;
;
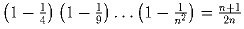 ;
;
- 1 • 2¹ + 2 • 2² + … + n • 2n = (n – 1) • 2n + 1 + 2
- 1³ + 2³ + … + n³ = (1 + 2 + … + n)².
Задача 5:
Докажите, что число 11 … 1 (3
n единиц) делится на 3
n.
Задача 6:
На сколько частей делят плоскость n прямых, среди которых нет параллельных и
никакие три не пересекаются в одной точке? (Прямые «общего положения»).
Задача 7:
На плоскости расположено несколько прямых и окружностей. Докажите, что
части, на которые они разбивают плоскость, можно покрасить в два цвета так,
что любые две части, имеющие общий участок границы, покрашены в разные
цвета.
Задача 8:
В прямоугольнике 3 × n (3 строки, n столбцов) расставлены фишки трех
цветов по n штук каждого цвета. Докажите, что переставляя фишки в строчках,
можно сделать так, чтобы в каждом столбце были фишки всех трех цветов.
Задача 9:
Отряд девочек отправился в поход. После того, как они вернулись, их
родителям стало известно, что хотя бы одна из них искупалась в походе без
разрешения, и каждый решил высечь свою дочь, если узнает о том, что она
купалась. Каждое утро девочки ходят в школу и обмениваются слухами о том,
кто искупался в походе и кого высекли родители, которые сообщают вечером
родителям (исключая информацию о том, купались ли они сами). Через 13 дней
несколько отцов, получив очередную порцию информацию, догадались о
провинности их дочерей и высекли их. Сколько детей получило в этот вечер
наказание?
Задача 10:
Можно ли отметить на плоскости несколько точек так, чтобы на расстоянии 1 от
каждой отмеченной точки находилось ровно 10 отмеченных?


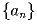 задана правилом:
a1 = 1, а каждый член, начиная со второго, вычисляется
по формуле an + 1 = 2an + 1. Докажите, что an = 2n – 1.
Задача 3:
Докажите, что любую сумму, начиная с 8 рублей, можно выплатить монетами по 3
рубля и 5 рублей.
Задача 4:
Доказать тождества:
задана правилом:
a1 = 1, а каждый член, начиная со второго, вычисляется
по формуле an + 1 = 2an + 1. Докажите, что an = 2n – 1.
Задача 3:
Докажите, что любую сумму, начиная с 8 рублей, можно выплатить монетами по 3
рубля и 5 рублей.
Задача 4:
Доказать тождества: 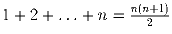 ;
; ;
; ;
;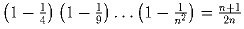 ;
;