 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Площади | Показать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Площади |
|
|
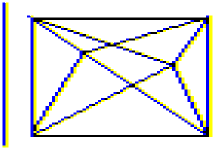
Задача 2: Докажите, что площадь тупоугольного треугольника равна половине произведения любой из его сторон на высоту, опущенную на эту сторону или ее продолжение из противолежащей вершины. Задача 3: Лариса Ивановна и Виктор Яковлевич делят квадратный пирог. Виктор Яковлевич отмечает внутри пирога точку, а Лариса Ивановна соединяет ее отрезками со всеми вершинами квадрата и забирает себе любые два куска, не имеющие общих сторон. Как должен действовать Виктор Яковлевич, чтобы получить побольше пирога? Задача 4: Внутри квадрата отметим две точки и соединим их отрезками со всеми вершинами (см. рис.). Могут ли все девять полученных частей иметь одинаковую площадь?
Задача 5: Докажите, что площадь параллелограмма ABCD равна произведению стороны AD на расстояние между прямыми AD и BC. Задача 6:
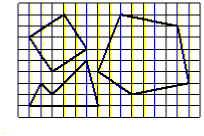
Найдите площади фигур, изображенных на рисунке.
Задача 7:
а) Через каждую вершину выпуклого четырехугольника проведена прямая, параллельная его диагонали. Докажите, что полученный параллелограмм по площади вдвое больше четырехугольника.
б) Середины соседних сторон выпуклого четырехугольника соединены отрезками. Докажите, что площадь полученного четырехугольника вдвое меньше площади данного.
Задача 8: Существует ли такой треугольник, что а) все его стороны больше 1 км, а площадь меньше 1 см²; б) все его высоты меньше 1 см, а площадь больше 1 км²; в) все стороны треугольника меньше 1 см, а его площадь больше 1 см². Задача 9: Докажите, что для площади S треугольника со сторонами a, b, c имеет место неравенство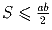 ;
Задача 10:
;
Задача 10: а) Докажите, что медиана разбивает треугольник на два равновеликих треугольника.
б) В треугольнике проведены все три медианы, которые разбивают его на шесть треугольников. Докажите, что площади полученных треугольников равны.
Докажите, что площадь трапеции равна произведению полусуммы оснований на расстояние между ними.
Задача 11: Квадрат разрезан прямыми, параллельными его сторонам, на прямоугольники, которые раскрашены в черный и белый цвета в шахматном порядке (см. рисунок) . При этом оказалось, что общая площадь черных прямоугольников равна площади белых прямоугольников. Докажите, что прямоугольники можно переместить так, что все черные прямоугольники составят один прямоугольник.

а) Докажите, что если AD параллельна BC, то треугольники ABO и CDO равновелики.
б) Докажите, что если треугольники ABO и CDO равновелики, то AD параллельна BC.
Задача 13: а) На основании равнобедренного треугольника выбрана точка, и из нее опущены перпендикуляры на боковые стороны. Докажите, что сумма длин этих перпендикуляров не зависит от выбора точки.б) Внутри равностороннего треугольника выбрана точка, и из нее опущены перпендикуляры на все три стороны. Докажите, что сумма длин этих перпендикуляров не зависит от выбора точки.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Площади | Показать решения |