 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Комбинаторика-1 | Показать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Комбинаторика-1 |
|
|
Задача 2: Сколько различных n-буквенных слов существует в языке племени Мумбо-Юмбо, если мумбоюмбский алфавит содержит 5 букв М, У, Б, О, Ю?
Задача 3: Строкой называется произвольная последовательность символов. Сколько различных строк можно получить, а) переставляя буквы в слове «КОТЕЛЬНИЧ»;
б) составляя девятизначное число из цифр от 1 до 9, используя все цифры.
Задача 4: Доказать, что Pn = n!.
Задача 5: Поезд состоит из трёх различных багажных вагонов (без номеров), четырёх плацкартных (с номерами от 1 до 4) и двух купейных (с номерами 5 и 6).
а) Сколькими способами можно сформировать состав, который начинается с вагона номер 1, а заканчивается вагоном номер 6?
б) Сколькими способами можно сформировать состав, в котором сначала идут все плацкартные вагоны, потом все купейные, а в конце – все багажные?
Задача 6: Сколько различных светящихся колец можно сделать, расположив по окружности 10 разноцветных лампочек (кольца считаются одинаковыми при одинаковом порядке следования цветов). Задача 7: Сколько есть перестановок чисел 1, 2, 3, …, 9, в которых цифры 4 и 8 стоят на своих местах? Задача 8: aaa Сколько есть перестановок чисел 1, 2, 3, …, 9, в которых цифры 1 и 2 не стоят рядом? Задача 9: Есть 12 шариков различных цветов и три различных ящика. Сколькими способами можно заполнить ящики шариками (по одному шарику в каждый ящик)?Задача 10: Доказать, что
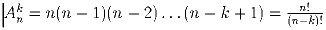 .
.Задача 11: Сколько способов выдать 10 различных нарядов кому-нибудь из 69 школьников (один наряд – один школьник). Задача 12: В выпуклом 20-угольнике провели все стороны и диагонали.
а) Сколько проведено линий?
б) Сколько треугольников (вершины которых являются вершинами исходного 20-угольника) при этом образовалось?
Задача 13: Сколькими способами можно выбрать троих дежурных в столовую из группы, в которой занимается 17 школьников? Задача 14: Из 15 семиклассников требуется выбрать на матбой семь человек – капитана и шесть остальных членов команды. Сколько существует различных выборов?
Задача 15: Докажите, что
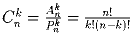 .
.Задача 16: Из цифр от 1 до 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4, 5 одновременно. Задача 17: У семиклассника Лени есть 7 книг по математике, а у восьмиклассника Бори – 8 книг. Сколькими способами они могут обменять три книги одного на три книги другого? Задача 18: Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трёх до десяти звуков? Задача 19: Во сколько раз
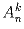 больше
больше 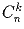 ?
Задача 20:
Двенадцати семиклассникам выданы два варианта контрольной
работы. Сколькими способами можно посадить учеников в два ряда по 6
человек, чтобы у сидящих рядом не было одинаковых вариантов, а у
сидящих друг за другом был один и тот же вариант.
Задача 21:
Пусть на диск сейфа нанесено 12 букв, а секретное слово состоит
из 5 букв. Сколько неудачных попыток может быть сделано человеком, не
знающим секретного слова?
Задача 22:
Сколькими способами может пригласить Констатин Александрович на
консультацию 7 семиклассников по 3 человека в течение 7 дней, так,
чтобы никакие 3 из них не встретились на консультации дважды?
?
Задача 20:
Двенадцати семиклассникам выданы два варианта контрольной
работы. Сколькими способами можно посадить учеников в два ряда по 6
человек, чтобы у сидящих рядом не было одинаковых вариантов, а у
сидящих друг за другом был один и тот же вариант.
Задача 21:
Пусть на диск сейфа нанесено 12 букв, а секретное слово состоит
из 5 букв. Сколько неудачных попыток может быть сделано человеком, не
знающим секретного слова?
Задача 22:
Сколькими способами может пригласить Констатин Александрович на
консультацию 7 семиклассников по 3 человека в течение 7 дней, так,
чтобы никакие 3 из них не встретились на консультации дважды?
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Комбинаторика-1 | Показать решения |