 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> ``Подумаешь, бином Ньютона!'' | Показать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. ``Подумаешь, бином Ньютона!'' |
|
|
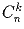 как число способов выбрать k (неупорядоченных)
предметов из n. Используя именно это определение (т.е. не пользуясь
формулой для числа сочетаний), докажите, что для любых «допустимых»
n и k (т.е. удовлетворяющих неравенству 0 ≤ k ≤ n) выполнены равенства:
как число способов выбрать k (неупорядоченных)
предметов из n. Используя именно это определение (т.е. не пользуясь
формулой для числа сочетаний), докажите, что для любых «допустимых»
n и k (т.е. удовлетворяющих неравенству 0 ≤ k ≤ n) выполнены равенства:а) 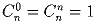 ;
;
б) 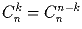 ;
;
в) 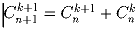 .
.
Задача 2: [Треугольник Паскаля] Расположите
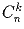 в виде таблицы, имеющей вид равнобедренного
треугольника (в верхней строке одно число, под ним два, затем три и т.п.)
Используя пункт в) предыдущей задачи, выпишите полученный вами треугольник
Паскаля до восьмой строки включительно.
в виде таблицы, имеющей вид равнобедренного
треугольника (в верхней строке одно число, под ним два, затем три и т.п.)
Используя пункт в) предыдущей задачи, выпишите полученный вами треугольник
Паскаля до восьмой строки включительно.Задача 3: Найдите сумму всех чисел n-ой строки треугольника Паскаля.
Указание: Вычислите её при нескольких небольших значениях n, угадайте общий результат, а для его доказательства примените метод математической индукции.
Задача 4: Сколько всего слагаемых получится после раскрытия скобок в выражении (1 + x)n
а) без приведения подобных слагаемых;
б) после приведения подобных слагаемых?
Задача 5: Сколькими способами можно выбрать произвольное непустое подмножество из множества, содержащего n элементов?
Указание: Сначала разберитесь с задачей без слова «непустое».
Задача 6: В каждой клетке квадрата 8 × 8 напишите количество кратчайших путей «хромой ладьи» из левой нижней клетки квадрата в эту клетку. (Хромая ладья ходит только на одну клетку вправо либо на одну клетку вверх). Какое число будет записано в правой верхней клетке?
Задача 7: Докажите, что произведение n последовательных натуральных чисел делится на n!.
Задача 8: Докажите, что для любого простого числа p число
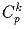 делится
на p при всех k, кроме k = 0 и k = p.
делится
на p при всех k, кроме k = 0 и k = p.Задача 9: [Бином Ньютона] Взгляните на равенства 1 = 1 • 1 • 1, x = x • 1 • 1 = 1 • x • 1 = 1 • 1 • x, x² = x • x • 1 = x • 1 • x = 1 • x • x, x³ = x • x • x. Они показывают, что если составлять произведения трёх множителей, каждый из которых равен 1 или x, то единицу и x³ можно получить единственным способом, а x и x² – тремя способами.
а) Сколькими способами можно представить xk в виде произведения n множителей, каждый из которых равен 1 или x?
б) Используя очевидное равенство (1 + x)n = (1 + x)(1 + x) … (1 + x) и результат пункта а), докажите формулу бинома Ньютона
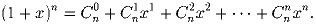
Задача 10: [Ещё раз бином Ньютона] Докажите методом математической индукции формулу бинома Ньютона.
Задача 11: Найдите коэффициент при x4 в разложении (1 + x)¹º.
Задача 12: С помощью бинома Ньютона докажите, что
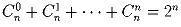 .
.Задача 13: Докажите, что
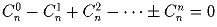 .
.Задача 14: Сколькими способами можно расставить в ряд n единиц и n минус единиц так, чтобы сумма любого количества подряд идущих чисел ряда, начиная с первого, была неотрицательной?
Задача 15: [n + n = 2n – часть 1] В куче лежит n синих и n красных шариков. Докажите, что количество способов взять из кучи ровно n шариков равно
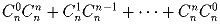 .
.
Указание: Разберитесь отдельно со случаями «0 синих шариков», «1 синий шарик», …, «n синих шариков».
Задача 16: [n + n = 2n – часть 2] Чему равен коэффициент при xn, который получается после раскрытия скобок
а) в выражении (1 + x)2n?
б) в выражении 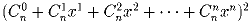 .
.
Задача 17: Сравните результаты, полученные в двух предыдущих задачах.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> ``Подумаешь, бином Ньютона!'' | Показать решения |