 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Неравенство треугольника | Показать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Неравенство треугольника |
|
|
Задача 2: Докажите, что длина любой стороны треугольника не превосходит его полупериметра.
Задача 3: Найдите внутри выпуклого четырёхугольника точку, такую, что сумма расстояний от нее до вершин минимальна.
Задача 4: Докажите, что
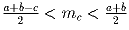 .
.Задача 5: Докажите, что в выпуклом четырёхугольнике сумма длин диагоналей больше его полупериметра и меньше периметра.
Задача 6: Докажите, что в выпуклом пятиугольнике сумма длин диагоналей больше периметра и меньше удвоенного периметра. Задача 7: Внутри треугольника взяли две произвольные точки. Докажите, что расстояние между ними не превосходит полупериметра треугольника.
Задача 8: На сторонах единичного квадрата отмечены 4 точки, по одной на каждой стороне. Докажите, что периметр образованного ими четырёхугольника больше двух.
Задача 9: В четырёхугольнике ABCD ∠ ADC = 90. Докажите, что 2DB ≤ PABC.
Задача 10: Грибник выходит из леса в заданной точке. Ему надо дойти до шоссе, которое представляет собой прямую линию, и зайти обратно в лес в другой заданной точке. Как ему сделать это, пройдя по самому короткому пути?
Задача 11: Точку M, лежащую внутри угла, отразили симметрично относительно сторон этого угла, в результате чего получились точки M1 и M2. Докажите, что внутри угла содержится не более половины отрезка M1M2.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Неравенство треугольника | Показать решения |