 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Геометрия-1. Площади | Показать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Геометрия-1. Площади |
|
|
Задача 2: Докажите, что площадь остроугольного треугольника равна половине произведения основания на высоту.
Задача 3: Докажите, что площадь тупоугольного треугольника равна половине произведения основания на высоту.
Задача 4: Докажите, что площадь параллелограмма равна произведению основания на высоту.
Задача 5: Докажите, что площадь трапеции равна половине произведения суммы двух оснований на высоту.
Задача 6: а) Докажите, что медиана делит треугольник на две равновеликие части.
б) Точка D лежит на стороне BC треугольника ABC.
Докажите, что 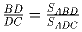 .
.
Задача 8: а) Точку пересечения медиан треугольника соединили со всеми вершинами. Докажите, что площади получившихся треугольников равны. Задача 9: В четырёхугольнике ABCD площади треугольников DBC и ADC равны. Докажите, что AB\|CD.
Задача 10: Диагонали делят трапецию на 4 треугольника. Докажите, что площади двух треугольников, прилегающих к боковым сторонам равны. Задача 11: В параллелограмме ABCD выбрана точка P. Докажите, что SABP + SCPD = SBCP + SDPA.
Задача 12: Дан выпуклый четырёхугольник, диагональ AC которого делит среднюю линию MN (M — середина BC, а N — AD) пополам. Докажите, что треугольники ABC и ACD — равновелики.
Задача 13: (Теорема Вариньона) а) Докажите, что фигура, образованная серединами сторон произвольного четырёхугольника — параллелограмм. б) Докажите, что площадь этого параллелограмма равна половине площади исходного четырёхугольника. Задача 14: Из точки внутри равностороннего треугольника опускаются перпендикуляры на стороны. Докажите, что сумма их длин не зависит от выбора точки. Задача 15: Средние линии четырёхугольника разделяют его на четыре четырёхугольника. Докажите, что суммы площадей несмежных четырёхугольников равны.
Задача 16: Докажите, что если одна из средних линий четырёхугольника делит его площадь пополам, то этот четырёхугольник – трапеция или параллелограмм.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Геометрия-1. Площади | Показать решения |