Задача 1:

x, y, z – вещественные числа. Докажите, что если

то x > 0, y > 0, z > 0.

Задача 2:

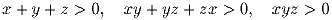
В треугольнике ABC медианы к сторонам AB и AC перпендикулярны. Докажите, что

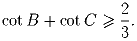
Задача 3:

Существуют ли на плоскости такие точки A, B и C, что для любой точки P на той же плоскости длины отрезков AP, BP и CP иррациональны.

Задача 4: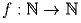

1. Существует ли такая функция , что f(f(n)) = 2n?

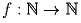2. Существует ли такая функция , что f(f(n)) = n + 2001?

Задача 5: Обозначим через P произведение всех простых чисел p таких, что n < p ≤ 2n. Докажите, что P < 4^n – 1.