Задача 1: Стороны треугольника равны a, b и c. Пусть p – полупериметр
треугольника (p = (a + b + c)/2). Строят треугольник со сторонами p – a, p – b
и p – c (если возможно), затем тоже самое делают с полученным
треугольником и так далее. Найдите все треугольники, для которых данный
процесс может продолжаться бесконечно.
Задача 2: Окружности с центрами в точках O1 и O2 касаются
окружности с центром O в точках A1 и A2, и
касаются друг друга в точке A. Докажите, что прямые AO,A1O1,A2O2
пересекаются в одной точке.
Задача 3: Пусть n – целое число большее 3. Выберем три различных числа из
множества 1,2, … ,n. Используя только эти три числа (каждое по
одному разу), а также операции сложения, умножения и расставления скобок
образуем все возможные арифметические выражения.
- [(1)] Докажите, что если все три выбранных числа больше n/2, то
значения всех составленных выражений различны.
- [(2)] Пусть p – простое число не превосходящее
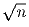 .
Докажите, что число способов выбрать три числа таких, что наименьшее из
них равно p и значения не всех полученных выраженний различны, в
точности равно количеству натуральных делителей числа p – 1.
.
Докажите, что число способов выбрать три числа таких, что наименьшее из
них равно p и значения не всех полученных выраженний различны, в
точности равно количеству натуральных делителей числа p – 1.
Задача 4: Найдите все пары чисел (h,s) такие что для любых h
прямых, параллельных данной прямой l, и s прямых таких, что
- [(1)] ни одна из них не параллельна l;
- [(2)] никакие две из них не параллельны;
- [(3)] никакие три из h + s прямых не пересекаются в одной точке
количество областей на которые эти h + s прямых делят плоскость равно
1992.
Задача 5: Найдите последовательность максимальной длины, состоящую из
ненулевых целых чисел, такую, что сумма любых семи членов
последовательности подряд была бы положительна, а любых одиннадцати членов
подряд – отрицательна.


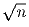 .
Докажите, что число способов выбрать три числа таких, что наименьшее из
них равно p и значения не всех полученных выраженний различны, в
точности равно количеству натуральных делителей числа p – 1.
.
Докажите, что число способов выбрать три числа таких, что наименьшее из
них равно p и значения не всех полученных выраженний различны, в
точности равно количеству натуральных делителей числа p – 1.