Задача 1: Найдите все функции заданные на множестве вещественных чисел,
удовлетворяющие следующим трем условиям:
- [(1)] для любых вещественных x,y
f(x) + f(y) + 1 ≥ f(x + y) ≥ f(x) + f(y);
- [(2)] для всех x ∈ [\,0,\,1\,), f(0) ≥ f(x);
- [(3)] – f( – 1) = f(1) = 1.
Задача 2: Докажите, что расстояние от ортоцентра невырожденного треугольника
до центра описанной вокруг него окружности строго меньше 3R, где R –
радиус описанной окружности.
Задача 3: Найдите все натуральные n, которые можно представить в виде суммы
квадратов двух взаимно простых чисел (n = a² + b²), таким образом, что
любое простое число 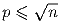 является делителем ab.
является делителем ab.
Задача 4: Существует ли бесконечное множество точек на плоскости такое, что
никакие три точки из него не лежат на одной прямой и все
попарные расстояния между ними рациональные?
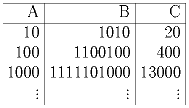
Задача 5: В таблице A записаны числа 10k (для всех k > 0) в десятичной
системе счисления, в таблице B они же записаны в двоичной, а в таблице
C – в пятеричной. Докажите, что каким бы ни было число n > 1, найдется
ровно одно число или в таблице B или в таблице C, в записи которого
ровно n цифр.


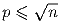 является делителем ab.
является делителем ab.