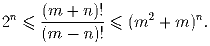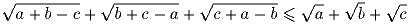Задача 1:

Стороны четырехугольника ABCD равны. MN и PQ – отрезки перпендикулярные диагонали BD, концы которых лежат на разных сторонах четырехугольника, а расстояние между ними d > BD/2. Докажите, что периметр шестиугольника AMNCQP зависит только от расстояния между отрезками MN и PQ и не зависит от положения отрезков.

Задача 2:

m и n – два натуральных числа и n ≤ m. Докажите, что

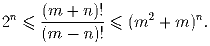
Задача 3:

P₁,P₂,P₃,P₄ – четыре точки на окружности. I₁ – центр окружности, вписанной в треугольник P₂P₃P₄, I₂ – центр окружности, вписанной в P₁P₃P₄. Аналогично определяются точки I₃ и I₄. Докажите, что точки I₁, I₂, I₃, I₄ являются вершинами прямоугольника.

Задача 4:

Национальный семейный совет хочет пригласить n супружеских пар для формирования 17 дискуссионных групп на следующих условиях:

• [(1)] все члены каждой группы должны быть одинакового пола;
• [(2)] количество человек в любых двух группах должно различаться не более чем на 1;
• [(3)] в каждой группе должен быть хотя бы один человек;
• [(4)] каждый человек должен быть в какой-нибудь группе.

Найдите все такие n ≤ 1996, при которых такое разбиение возможно.

Задача 5:

a,b,c – стороны треугольника. Докажите, что

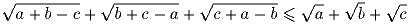
и определите, в каких случаях будет иметь место равенство.