Задача 1: Найдите все функции 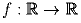 такие, что
f(xf(x) + f(y)) = (f(x))² + y для любых вещественных чисел x и y.
такие, что
f(xf(x) + f(y)) = (f(x))² + y для любых вещественных чисел x и y.
Задача 2: На медиане AD неравнобедренного треугольника ABC взята точка E.
Точка F – проекция точки E на прямую BC, точка M лежит на отрезке
EF, точки N и P – проекции точки M на прямые AC и AB
соответственно. Докажите, что прямые, содержащие биссектрисы углов
PMN и PEN параллельны.
Задача 3: Найдите максимальное количество прямоугольников 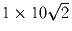 ,
которые можно вырезать из прямоугольника 50 × 90 с
помощью разрезов, параллельных его сторонам.
,
которые можно вырезать из прямоугольника 50 × 90 с
помощью разрезов, параллельных его сторонам.
Задача 4: Будем говорить, что натуральное число r является степенью, если
его можно представить в виде r = ts, где t и s – натуральные числа,
не равные 1. Докажите, что для любого натурального числа n существует
n степеней таких, что сумма любых k из них (1 < k ≤ n) также
является степенью.


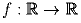 такие, что
f(xf(x) + f(y)) = (f(x))² + y для любых вещественных чисел x и y.
такие, что
f(xf(x) + f(y)) = (f(x))² + y для любых вещественных чисел x и y.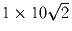 ,
которые можно вырезать из прямоугольника 50 × 90 с
помощью разрезов, параллельных его сторонам.
,
которые можно вырезать из прямоугольника 50 × 90 с
помощью разрезов, параллельных его сторонам.