 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 1 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 1 олимпиада |
|
|
Докажите, что дробь 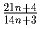 несократима при всех
натуральных n.
несократима при всех
натуральных n.
Определите, при каких вещественных x
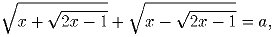
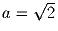 , b) a = 1, c) a = 2. (
, b) a = 1, c) a = 2. (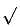 обозначает
неотрицательный квадратный корень из неотрицательного числа)
Задача 3:
обозначает
неотрицательный квадратный корень из неотрицательного числа)
Задача 3: a,b,c – вещественные числа. Дано уравнение a cos ²x + b cos x + c = 0. Составьте квадратное относительно cos 2x уравнение с теми корнями.
Задача 4:Постройте прямоугольный треугольник ABC по гипотенузе AC, медиана AM которого, удовлетворяет соотношению AM² = AB • AC.
Задача 5:На отрезке AB выбрали точку M. Вокруг квадратов AMCD и MBEF, лежащих по одну сторону от AB, описали окружности с центрами P и Q, которые пересекаются в точках M и N.
a) докажите, что AF и BC пересекаются в точке N;
b) докажите, что все прямые MN имеют общую точку;
c) определите геометрическое место середин отрезков PQ.
Задача 6:На непараллельных плоскостях α и β выбрали точки A и C соответственно, притом точки не лежат в пересечении плоскостей. Постройте точки B ∈ α и D ∈ β такие, что A,B,C,D лежат в одной плоскости, AB\|CD, AD = BC и четырехугольник ABCD – описанный.
| Задачная база >> Международные соревнования >> Международная МО >> 1 олимпиада | Показать решения |