 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 3 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 3 олимпиада |
|
|
Найдите x,y,z удовлетворяющих системе уравнений:
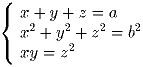
Задача 2:
a,b,c – стороны треугольника площади S. Докажите, что
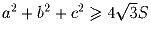 и определите, когда достигается равенство?
и определите, когда достигается равенство?
Задача 3:
Решите уравнение cos nx – sin nx = 1.
Задача 4:
Внутри треугольника ABC взяли точку P. Прямые PA, PB и PC пересекают стороны треугольника в точках D,E и F соответственно. Докажите, что по крайней мере одно из отношений AP/PD,BP/PE,CP/PF не превосходит 2, и по крайней мере одно не больше 2.
Задача 5:Постройте треугольник ABC по сторонам AC = b, AB = c и углу ∠ AMB = α , где M – середина BC. Докажите, что построение возможно тогда и только тогда, когда справедливо неравенство b tg ( α /2) ≤ c < b и определите, когда достигается равенство.
Задача 6:Даны точки A,B,C не лежащие на одной прямой, и плоскость α не параллельная плоскости ABC. В плоскости α взяли точки A′,B′ и C′. A″,B″,C″ – серидины отрезков AA′,BB′ и CC′ соответственно. Найдите геометрическое место центров тяжести треугольников A″B″C″.
| Задачная база >> Международные соревнования >> Международная МО >> 3 олимпиада | Показать решения |