 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 20 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 20 олимпиада |
|
|
Последние три цифры десятичной записи чисел 1978n и 1978m совпадают. Найдите такие m и n (m < n) с минимальной суммой.
Задача 2:Пусть P – данная точка внутри данной сферы и A,B,C – произвольные три точки этой сферы такие, что отрезки PA, PB, PC взаимно перпендикулярны. Пусть Q – вершина параллелепипеда, определенного отрезками PA, PB и PC, диагонально противоположная к P. Определите геометрическое место точек Q.
Задача 3:Множество всех натуральных чисел является объединением двух непересекающихся подмножеств f(1),f(2), … ,f(n), … , g(1),g(2), … ,g(n), … , где f(1) < f(2) < … < f(n) < … , g(1) < g(2) < … < g(n) < … и g(n) = f(f(n)) + 1 для всех n ≥ 1. Определите f(240).
Задача 4: Окружность касается внутренним образом окружности, описанной вокруг равнобедренного треугольника ABC, а также равных сторон AB и AC этого треугольника в точках P, Q соответственно. Докажите, что середина отрезка PQ является центром окружности, вписанной в треугольник ABC. Задача 5:ak – последовательность, состоящая из различных натуральных чисел. Докажите, что
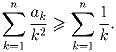
Задача 6:
Международное общество состоит из представителей шести различных стран. Список членов общества из 1978 фамилий, занумерованных числами 1,2, … ,1978. Докажите, что существует хотя бы один член общества, номер которого равняется сумме номеров двух членов из его страны или удвоенному номеру некоторого члена из его страны.
| Задачная база >> Международные соревнования >> Международная МО >> 20 олимпиада | Показать решения |