Задача 1:
[Великобритания] Из точки P внутри данного треугольника
ABC опускаются перпендикуляры PA
1, PB
1, PC
1 на прямые BC,
CA и AB. Для каких точек P внутри ∠ ABC величина
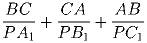
принимает наименьшее значение?
Задача 2:
[ФРГ] Даны натуральные числа n и r, 1 ≤ r ≤ n.
Рассмотрим всевозможные подмножества множества 1,2, … ,n,
состоящие из r чисел, и в каждом выберем наименьшее число.
Докажите, что среднее арифметическое всех выбранных чисел равно
(n + 1)/(r + 1). (Например, при n = 3, r = 2 получаем три
подмножества 1,2, 1,3, 2,3 и среднее
арифметическое равно (1 + 1 + 2)/3 = 4/3).
Задача 3:
[Нидерланды] Найдите наибольшее значение выражения m² + n²
для всевозможных пар (m,n) натуральных чисел таких, что 1 ≤ m ≤ 1981, 1 ≤ n ≤ 1981 и |n² – mn – m²| = 1.
Задача 4:
[Бельгия] а) Для каких n ≥ 3 существует множество из n
последовательных натуральных чисел, обладающих следующим
свойством: наибольшее из этих n чисел является делителем
наименьшего общего кратного остальных n – 1 чисел?
б) При каких n ≥ 3 существует единственное множество из n
последовательных чисел, обладающее указанным свойством?
Задача 5:
[СССР] Через точку O, лежащую внутри данного треугольника,
проведены три окружности равных радиусов, каждая из которых лежит
внутри треугольника и касается двух его сторон. Докажите, что
точка O, центр окружности, описанной около треугольника и центр
окружности, вписанной в него, лежат на одной прямой.
Задача 6:
[Франция] Про функцию f, определенную на множестве
всех пар неотрицательных целых чисел (x,y), известно
следующее:
1) f(0,y) = y + 1
2) f(x + 1,0) = f(x,1)
3) f(x + 1,y + 1) = f(x,f(x + 1,y))
для каждой пары x ≥ 0, y ≥ 0. Найдите значение f(4,1981).