Задача 1: [Великобритания] Дан выпуклый четырехугольник ABCD, вокруг которого можно описать окружность. Некоторая окружность с центром на стороне AB касается остальных трех сторон. Докажите, что |AD| + |BC| = |AB|.

Задача 2: [Австралия] Даны взаимно простые целые числа n и k (0 < k < n). Каждое из чисел множества M = 1,2, … ,n – 1 окрашивают либо в голубой, либо в белый цвет, так чтобы выполнялись следующие условия:

а) для каждого i из множества M числа i и n – i должны быть окрашены в один цвет;

б) для каждого i из M, отличного от k, числа i и |k – i| должны быть окрашены в один цвет.

Докажите, что все числа множества M будут окрашены в один цвет.

Задача 3: [Нидерланды] Для любого многочлена P(x) = a₀ + a₁x +  …  + a_kx^k с целыми коэффициентами обозначим через w(P) число нечетных коэффициентов. Пусть Q_i(x) = (1 + x)ⁱ для i = 0,1,2, …  Докажите, что если целые числа i₁, i₂,…, i_n удовлетворяют условию 0 ≤ i₁ < i₂ <  …  < i_n, то

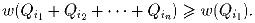
Задача 4: [Монголия] Дано множество M, состоящее из 1985 различных натуральных чисел. Простые делители каждого числа из множества M не превосходят 26. Докажите, что из множества M можно выбрать 4 попарно различных числа, произведение которых является четвертой степенью некоторого натурального числа.

Задача 5: [СССР] Дан треугольник ABC и окружность с центром O, проходящая через вершины A и C, которая повторно пересекает отрезки AB и BC в различных точках K и N соответственно. Окружности, описанные вокруг треугольников ABC и KBN, имеют ровно две общие точки B и M. Докажите, что угол OMB прямой.

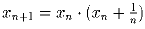
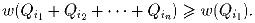
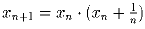Задача 6: [Швеция] Для каждого действительного числа x₁ строим последовательность x₁,x₂, … , полагая для всех n ≥ 1. Докажите, что существует одно и только одно значение x₁, для которого 0 < x_n < x_n + 1 < 1 при всех n.