 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 36 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 36 олимпиада |
|
|
Пусть A, B, C и D – четыре различные точки на прямой, расположенные в указанном порядке. Окружности с диаметрами AC и BD пересекаются в точках X и Y. Прямые XY и BC пересекаются в точке Z. Пусть P – точка на прямой XY, отличная от Z. Прямая CP пересекает окружность с диаметром AC в точках C и M, а прямая BP пересекает окружность с диаметром BD в точках B и N. Доказать, что прямые AM, DN и XY пересекаются в одной точке.
Задача 2:Пусть a,b,c – положительные действительные числа такие, что abc = 1. Доказать, что
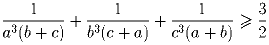
Найти все целые n > 3, для которых существуют n точек A1,A2, … An на плоскости и действительные числа r1,r2, … ,rn удовлетворяющие следующим двум условиям:
a) никакие три точки не лежат на одной прямой;
b) для любой тройки i,j,k площадь треугольника AiAjAk равна ri + rj + rk.
Задача 4:Найти наибольшее значение x0, для которого существует последовательность положительных действительных чисел x0,x1, … ,x1995, удовлетворяющих следующим двум условиям:
a) x0 = x1995
b) 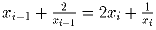 при всех i = 1,2, … ,1995.
при всех i = 1,2, … ,1995.
Пусть ABCDEF – выпуклый шестиугольник, в котором AB = BC = CD, DE = EF = FA и ∠ BCD = ∠ EFA = 60. Пусть G и H – две точки внутри шестиугольника такие, что ∠ AGB = ∠ DHE = 120 Доказать, что AG + GB + GH + DH + HE ≥ CF.
Задача 6:Пусть p – нечетное простое число. Найти количество подмножеств A множества 1,2, … ,2p таких, что:
a) A содержит ровно p элементов;
b) сумма вмех элементов из A делится на p.
| Задачная база >> Международные соревнования >> Международная МО >> 36 олимпиада | Показать решения |