Задача 1:

Пусть O – центр описанной окружности остроугольного треугольника ABC, AP – высота. Докажите, что если  ∠ BCA ≥  ∠ ABC + 30, то  ∠ CAB +  ∠ COP < 90.

Задача 2: Докажите, что

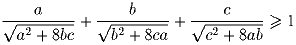
для всех положительных вещественных чисел a, b и c.

Задача 3: Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе.

• Каждый участник решил не более шести задач.
• Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими.

Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.

Задача 4: Пусть N – нечетное натуральное число большее 1, а k₁, k₂,…k_n – произвольные целые числа. Для каждой из n! перестановок a = (a₁,a₂, … ,a_n) чисел 1, 2,…n, обозначим

Докажите, что найдутся две такие перестановки b и c (b ≠ c), что n! является делителем S(b) – S(c).

Задача 5: В треугольнике ABC проведена биссектрисы AP и BQ. Известно, что  ∠ BAC = 60 и что AB + BP = AQ + QB. Какими могут быть углы треугольника ABC?

Задача 6: Пусть a, b, c, d – целые числа такие, что a > b > c > d > 0. Предположим, что ac + bd = (b + d + a – c)(b + d – a + c). Докажите, что число ab + cd составное.