Задача 1:
Числа p и q различны. Известно, что можно подобрать
такое число x, что x² + px + q = 0 и x² + qx + p = 0. Найдите p + q.
Задача 2:
Взяли 100 чисел. Среди их всевозможных произведений по
два числа оказались 1000 отрицательных. Сколько среди исходных чисел было
нулей?
Задача 3:
Найдите угол между прямыми, заданными уравнениями
y = 2x + 1 и
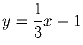
.
Задача 4:
В четырехугольнике ABCD углы A и C прямые. Из
точек B и D опустили перпендикуляры на диагональ AC и
получили соответственно точки M и N.
Докажите, что AN = CM.
Задача 5:
В какое наибольшее число цветов можно раскрасить клетки доски
8 × 8 так, чтобы у каждой клетки среди ее соседей (по
стороне) были хотя бы две клетки, окрашенные в тот же цвет?


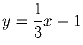 .
Задача 4:
В четырехугольнике ABCD углы A и C прямые. Из
точек B и D опустили перпендикуляры на диагональ AC и
получили соответственно точки M и N.
Докажите, что AN = CM.
Задача 5:
В какое наибольшее число цветов можно раскрасить клетки доски
8 × 8 так, чтобы у каждой клетки среди ее соседей (по
стороне) были хотя бы две клетки, окрашенные в тот же цвет?
.
Задача 4:
В четырехугольнике ABCD углы A и C прямые. Из
точек B и D опустили перпендикуляры на диагональ AC и
получили соответственно точки M и N.
Докажите, что AN = CM.
Задача 5:
В какое наибольшее число цветов можно раскрасить клетки доски
8 × 8 так, чтобы у каждой клетки среди ее соседей (по
стороне) были хотя бы две клетки, окрашенные в тот же цвет?