 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 7 класс | Показать решения |
|
|
| 64 Московская математическая олимпиада. Городской тур. 7 класс |
|
|
В книге рекордов Гиннесса написано, что наибольшее известное простое число равно 23021377 – 1. Не опечатка ли это?
(С. Маркелов)
Задача 2:Приходя в тир, игрок вносит в кассу 100 рублей. После каждого удачного выстрела количество его денег увеличивается на 10, а после каждого промаха уменьшается на 10. Могло ли после нескольких выстрелов у него оказаться 80 рублей 19 копеек?
(И. Ященко)
Задача 3:Для постройки типового дома не хватало места. Архитектор изменил проект: убрал 2 подъезда и добавил 3 этажа. При этом количество квартир увеличилось. Он обрадовался и решил убрать еще 2 подъезда и добавить еще 3 этажа. Могло ли при этом квартир стать даже меньше, чем в типовом проекте? (В каждом подъезде одинаковое число этажей, а на всех этажах во всех подъездах одинаковое число квартир.)
(T. Голенищева-Кутузова, В. Гуровиц, П. Кожевников, И. Ященко)
Задача 4:В стене имеется маленькая дырка (точка). У хозяина есть флажок следующей формы (см. рисунок). Покажите на рисунке все точки, в которые можно вбить гвоздь, так чтобы флажок закрывал дырку.
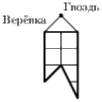
(А. Шень)
Задача 5:Отметьте на доске 8 × 8 несколько клеток так, чтобы любая (в том числе и любая отмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.
(А. Спивак)
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 7 класс | Показать решения |