 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 9 класс | Показать решения |
|
|
| 64 Московская математическая олимпиада. Городской тур. 9 класс |
|
|
Можно ли расставить на футбольном поле четырёх футболистов так, чтобы попарные расстояния между ними равнялись 1, 2, 3, 4, 5 и 6 метров?
(А. Митягин)
Задача 2:В некоторой стране суммарная зарплата 10 самых высокооплачиваемых работников составляет 90 зарплаты всех работников. Может ли так быть, что в каждом из регионов, на которые делится эта страна, зарплата любых 10 работников составляет не более 11 всей зарплаты, выплачиваемой в этом регионе?
(М. Вялый)
Задача 3:Внутри угла с вершиной M отмечена точка A. Из этой точки выпустили шар, который отразился от одной стороны угла в точке B, затем от другой стороны в точке C и вернулся в A («угол падения» равен «углу отражения»). Докажите, что центр O окружности, описанной около треугольника BCM, лежит на прямой AM.
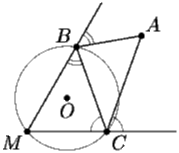
(А. Заславский)
Задача 4:Камни лежат в трёх кучках: в одной – 51 камень, в другой – 49 камней, а в третьей – 5 камней. Разрешается объединять любые кучки в одну, а также разделять кучку из чётного количества камней на две равные. Можно ли получить 105 кучек по одному камню в каждой?
(В. Клепцын)
Задача 5:Натуральное число N в 999 … 99 (k девяток) раз больше суммы своиx цифр. Укажите все возможные значения k и для каждого из них приведите пример такого числа.
(Г. Гальперин)
Задача 6:Участники шахматного турнира сыграли друг с другом по одной партии. Для каждого участника A было подсчитано число набранных им очков (за победу дается 1 очко, за ничью – 1/2 очка, за поражение – 0 очков) и коэффициент силы по формуле: сумма очков тех участников, у кого A выиграл, минус сумма очков тех, кому он проиграл.
а) Могут ли коэффициенты силы всех участников быть больше 0?
б) Могут ли коэффициенты силы всех участников быть меньше 0?
(А. Толпыго)
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 9 класс | Показать решения |