Задача 1:
Из пункта A в пункт B одновременно выехали
«Мерседес» и «Запорожец». Проехав треть пути, «Запорожец» остановился
и тронулся с места только тогда, когда «Мерседесу» оставалось проехать треть
пути до B. Доехав до B, «Мерседес» развернулся и поехал обратно
в A. Какой из автомобилей приедет раньше: «Мерседес» – в пункт
A или «Запорожец» – в пункт B?
Задача 2:
Числа x и y положительны, x + y = 6.
Найдите наименьшее возможное значение суммы
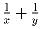
.
Задача 3:
Дано два непересекающихся круга. Существует ли вне
этих кругов такая точка, что всякая прямая, проходящая через неё, пересекает
хотя бы один из данных кругов?
Задача 4:
Оля и Коля играют на доске размером 9 × 9 клеток.
Первым ходом Оля закрашивает произвольную неугловую клетку.
Далее игроки по очереди закрашивают по одной клетке, примыкающей к любой из
уже закрашенных. Побеждает тот, кто первым закрасит одну из угловых клеток.
Кто выиграет при правильной игре и как он должен играть?
Задача 5:
Через точку пересечения медиан треугольника ABC
проходит прямая, пересекающая стороны AB и AC.
Расстояния от вершин B и C до этой прямой равны
b и c соответственно. Найдите расстояние от вершины
A до данной прямой.
Задача 6:
Сравните числа A и B, не пользуясь калькулятором:
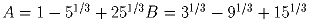


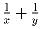 .
.