Задача 1:
(5–7)
В каждой клетке прямоугольной таблицы размером
M × K написано число. Сумма чисел в каждой строке и в
каждом столбце равна 1. Докажите, что M = K.
Задача 2:
(5–6)
В круге отметили точку. Разрежьте круг на а) три; б) две части так,
чтобы из них можно было составить новый круг, у которого
отмеченная точка будет в центре.
Задача 3:
(5–9)
Известно, что доля блондинов среди голубоглазых больше,
чем доля блондинов среди всех людей. Что больше — доля
голубоглазых среди блондинов или доля голубоглазых среди всех
людей?
Задача 4:
(5–6)
Можно ли нарисовать эту картинку (рис. 2), не отрывая
карандаша от бумаги и проходя по каждой линии по одному разу?
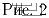
Задача 5:
(5–6)
Прямая раскрашена в два цвета. Докажите, что на ней
найдутся три точки A, B и C, окрашенные в один цвет такие,
что точка B является серединой отрезка AC.
Задача 6:
(7)
Пусть A, B и C — три числа, большие 0 и меньшие 1,
K — наибольшее из них. Докажите, что
1 – (1 – A)(1 – B)(1 – C) > K
Задача 7:
(7–9)
В треугольнике две высоты не меньше сторон, на которые
они опущены. Найдите углы треугольника.
Задача 8:
(7)
На плоскости нарисовано некоторое количество равносторонних
треугольников. Они не пересекаются, но могут иметь общие участки
сторон. Мы хотим покрасить каждый треугольник в какой-нибудь цвет
так, чтобы те из них, которые соприкасаются, были покрашены в
разные цвета (треугольники, имеющие одну общую точку, могут быть
покрашены в один цвет). Хватит ли для такой раскраски двух
цветов?
Задача 9:
(8–9)
Доказать неравенство
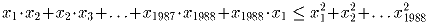
Задача 10:
(8–9)
В алфавите племени Мумбу-Юмбу есть лишь две буквы A и Б.
Два разных слова обозначают одно и то же понятие, если одно из
них может быть получено из другого с помощью следующих операций:
— в любом месте слова комбинацию букв АБА можно заменить на
БАБ;
— из любого места можно выкидывать две одинаковые буквы, идущие
подряд.
Может ли дикарь племени сосчитать все пальцы на своей руке? А дни
недели?