 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Болгария >> 1999 >> 4 тур | Показать решения |
|
|
| Болгарская математическая олимпиада.. 1999. 4 тур |
|
|
Грани параллелепипеда, длины ребер которого – целые числа, покрашены в зеленый цвет. Параллелепипед разрезали на единичные кубики, притом ровно треть из них не имеет ни одной зеленой грани. Найдите размеры параллелепипеда.
Задача 2:
Последовательность an удовлетворяет соотношению (n – 1)an + 1 = (n + 1)an – 2(n – 1). Известно, что a1999 делится на 2000. Найдите наименьшее k для которого ak делится на 2000.
Задача 3:
Одна из сторон треугольника с вершинами в узлах целочисленной решетки равна
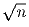 , где n не делится на квадрат никакого натурального числа большего 1.
Докажите, что отношение радиусов вписанной и описанной окружностей –
иррациональное число.
, где n не делится на квадрат никакого натурального числа большего 1.
Докажите, что отношение радиусов вписанной и описанной окружностей –
иррациональное число.
Задача 4:
Найдите количество натуральных чисел не превосходящих 1023 двоичная запись которых не содержит трех одинаковых цифр подряд.
Задача 5:
Вершины A, B и C остроугольного треугольника ABC лежат на сторонах B1C1, A1C1 и A1B1 треугольника A1B1C1 соответственно, притом ∠ ABC = ∠ A1B1C1, ∠ BCA = ∠ B1C1A1 и ∠ BAC = ∠ B1A1C1. Докажите, что ортоцентры треугольников ABC и A1B1C1 равноудалены от окружности описанной около треугольника ABC.
Задача 6:
Докажите, что уравнение x³ + y³ + z³ + t³ = 1999 имеет бесконечно много решений в целых числах.
| Задачная база >> Национальные зарубежные олимпиады >> Болгария >> 1999 >> 4 тур | Показать решения |