 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1972 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1972 |
|
|
Три единичные окружности касаются друг друга. Найдите радиус окружности касающейс всех трех.
Задача 2:a1,a2, … ,an – неотрицательные вещественные числа. M – сумма их попарных произведений. Докажите, что квадрат по крайней мере одного из чисел ai не превосходит 2M/n(n – 1).
Задача 3:a) Докажите, что число 10201 составное в любой системе счислени с основанием больше 2.b) Докажите, что число 10101 составное в любой системе счисления.
Задача 4:
Постройте четырехугольник ABCD по длинам четырех сторон, если известно, что AB\|CD,а BC и DA не пересекаются.
Задача 5:Докажите, что уравнение x³ + 11³ = y³ не имеет решений в натуральных числах.
Задача 6:
a и b – различные вещественные числа. Докажите, что существуют такие целые числа m и n, что am + bn > 0, а bm + an < 0.
Задача 7:a) Докажите, что корни уравнения x = (x² + 1)/198 находятс
между 1/198 и 197,99494949 … b) Используя a) докажите, что 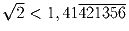 ;c) Верно ли, что
;c) Верно ли, что 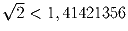 ?
?
В предвыборной кампании участвовало несколько партий, которые в сумме пообещали p обещаний. Известно, что у любых двух партий по крайней мере по одному обещанию совпало и никакие две партии не пообещали одного и того же. Докажите, что количество партий не больше 2p – 1.
Задача 9:Прямые l1 и l2 соответственно параллельны прямым l3 и l4. Найдите геометрическое место точек сумма расстояний от которых до этих прямых постоянна.
Задача 10:Найдите геометрическую прогрессию максимальной длины все члены которой – целые числа из промежутка от 100 до 1000.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1972 | Показать решения |