 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1984 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1984 |
|
|
Докажите, что сумма 1984 последовательных натуральных чисел не может быть точным квадратом.
Задача 2:
В какое наименьшее количество цветов нужно раскрасить n ключей так, чтобы не путать их между собой, если все n ключей находятся одном кольце?
Задача 3:
Докажите, что существует бесконечно много натуральных чисел, ни одна цифра которых не равна 0, и которые делятся на сумму своих цифр.
Задача 4:
Площадь остроугольного треугольника равна 1. Докажите, что внутри
треугольника найдется точка такая, что расстояние от нее до каждой
вершины не более 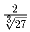 .
.
Задача 5:
Дано 7 вещественных чисел. Докажите, что среди них найдутся два числа x и y такие, что
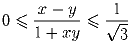
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1984 | Показать решения |