Задача 1: На стороне AD треугольника ABD взяли точку C такую, что ∠ ABC = 90,
∠ CBD = 30, |AB| = |CD| = 1. Найдите |AC|.
Задача 2: В соревновании, состоящим из M состязаний участвовали A,B и C.
За первое место в любом состязании присуждалось p1, за второе – p2, за
третье – p3 очков, где p1 > p2 > p3 > 0 и все pi целые. В итоге A набрал
22, а B и C – по 9 очков. B победил в забеге на 100 метров. Найдите
M и определите, кто был вторым в прыжке в высоту.
Задача 3: На полуокружности диаметром AB выбрали хорду ST длины a. M – середина
ST, P – основание перпендикуляра, опущенного из точки P на AB.
Докажите, что величина угла SPM не зависит от положения хорды ST.
Задача 4: 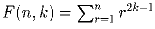 . Докажите, что F(n,k) делится на F(n,1).
. Докажите, что F(n,k) делится на F(n,1).
Задача 5: Последовательность un задана рекуррентно:
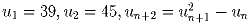 . Докажите, что бесконечно много
членов последовательности делится на 1986.
. Докажите, что бесконечно много
членов последовательности делится на 1986.


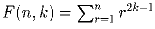 . Докажите, что F(n,k) делится на F(n,1).
. Докажите, что F(n,k) делится на F(n,1).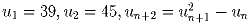 . Докажите, что бесконечно много
членов последовательности делится на 1986.
. Докажите, что бесконечно много
членов последовательности делится на 1986.