 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Эстонская МО >> 1995 >> 10 класс | Показать решения |
|
|
| Национальные зарубежные олимпиады. Эстонская МО. 1995. 10 класс |
|
|
Найти все целые числа n такие, что (n² + n – 1)n + 3 = 1.
Задача 2:В правильном треугольнике расположены три окружности одинакового радиуса, как показано на рисунке. Найти отношение длины стороны треугольника a к радиусу окружности r.
Задача 3:Пусть p,q – целые числа и x1,x2 – решения квадратного
уравнения x² + px + q = 0. Возможно ли, что 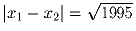 ?
?
Найти площадь заштрихованной на рисунке области, если вершина C треугольника находится в центре окружности, |BC| = 1 и ∠ BAC = 30.
Рисунок временно утерян ;(
Задача 5:Найти все вещественные решения системы уравнений
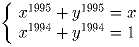
На классном вечере каждый мальчик танцевал по крайней мере с половиной девочек, а каждая девочка – не более, чем с половиной мальчиков. Доказать, что как девочек, так и мальчиков на классном вечере было четное число.
| Задачная база >> Национальные зарубежные олимпиады >> Эстонская МО >> 1995 >> 10 класс | Показать решения |