Задача 1: В остроугольном треугольнике ABC угол A равен 30, H – ортоцентр треугольника, M – середина стороны BC. На прямой MT выбрали точку H такую, что HM = MT. Докажите, что AT = 2BC.

Задача 2: Докажите, что существует бесконечно много пар целых взаимно простых чисел (a,b) таких, что квадратные трехчлены x² + ax + b и x² + 2ax + b оба имеют целые корни.

Задача 3: Докажите, что среди трехэлементных подмножеств множества 1,2, … ,63 подмножеств с суммой элементов меньше 95 меньше, чем с суммой больше 95.

Задача 4: Окружность  Γ ′ внешним образом касается окружности  Γ , вписанной в треугольник ABC и сторон AB и AC. Докажите, что отношение радиусов  Γ ′ и  Γ  равно .

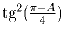
Задача 5: a₁,a₂, … ,a_n – вещественные числа большие 1, притом |a_k – a_k + 1| < 1 для всех 1 ≤ k ≤ n – 1. Докажите, что

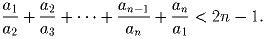
Задача 6: Найдите все простые p для которых число (2^p – 1 – 1)/p является точным квадратом.
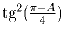