 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Индия >> Индийская олимпиада. >> 1997 | Показать решения |
|
|
| Национальные зарубежные олимпиады. Индия. Индийская олимпиада.. 1997 |
|
|
Прямая, проходящая через вершину C параллелограмма ABCD пересекает продолжения сторон AB и AD в точках E и F соответственно. Докажите, что AC² + CE • CF = AB • AE + AD • AF.
Задача 2:
Докажите, что не существует натуральных n и m таких, что
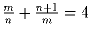 .
.
Задача 3: a,b,c – различные вещественные числа, притом
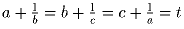 .
Докажите, что abc + t = 0.
.
Докажите, что abc + t = 0.Задача 4: Единичный квадрат разбили на 100 частей отрезками, выходящими из центра. Оказалось, что периметры всех частей одинаковы и равны p. Докажите, что 1,4 < p < 1,5.
Задача 5: Каким количеством способов можно расставить числа от 0 до 3 в таблице 4 × 4 так, чтобы сумма чисел в каждой строке и в каждом столбце делилась бы на 4?
Задача 6: a и b – положительные вещественные числа такие, что все корни уравнения x³ – ax + b = 0 вещественны. Пусть α – один из них. Докажите, что
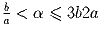 .
.
| Задачная база >> Национальные зарубежные олимпиады >> Индия >> Индийская олимпиада. >> 1997 | Показать решения |