Задача 1:
В окружности Γ с центром в точке O провели
отличную от диаметра хорду AB. Точка M – середина
AB. Касательная к окружности Γ
1, построенной на OM как
на диаметре пересекает Γ в точке P. Пусть T –
точка ее касания с Γ
1.
Докажите, что PA² + PB² = 4PT².
Задача 2:
Числа, a, b и
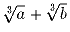
– рациональные.
Докажите, что числа
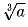
и
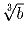
также
рациональные.
Задача 3:
a,p,q,r,s – целые числа, притом, s не делится на 5,
а pa³ + qa² + ra + s делится на 5.
Докажите, что существует такое натуральное число b,
что sb³ + rb² + qb + p делится на 5.
Задача 4:
Вершины четырехугольника ABCD лежат на окружности радиуса 1, притом
AB • BC • CD • DA ≥ 4. Докажите, что ABCD –
квадрат.
Задача 5:
Корни уравнения x² – (a + b + c)x + (ac + bc + ca) = 0 комплексны
и имеют вид α ± i β , притом α > 0.
Докажите, что числа a, b и c положительные,
а из отрезков длины
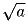
,
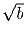
,
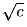
можно составить треугольник.
Задача 6:
Из набора 0,0,1,1,2,2, … ,n – 1,n – 1 выбирают n
чисел таких, что их среднее арифметическое A
n – целое.
Найдите минимальное значение A
n в зависимости от n.


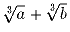 – рациональные.
Докажите, что числа
– рациональные.
Докажите, что числа 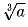 и
и 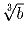 также
рациональные.
также
рациональные.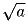 ,
, 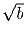 ,
, 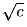 можно составить треугольник.
можно составить треугольник.