Задача 1: Стороны треугольника – последовательные натуральные числа, а радиус вписанной окружности равен 4. Найдите радиус окружности описанной около этого треугольника.

Задача 2: Найдите все тройки натуральных чисел (a,b,c) таких, что

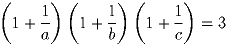
Задача 3: Решите систему в вещественных числах:

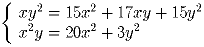
Задача 4: Сумма любых трех последовательных цифр n-значного числа N делится на 5. Докажите, что если все цифры N различны, то n ≤ 6. Также, докажите, что можно найти шестизначное число обладающее данным свойством, начинающееся с любой цифры.

Задача 5: a,b,c – стороны треугольника, h_a – высота, проведенная к стороне a. Докажите, что .

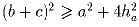Задача 6: Докажите, что для любого n существуют положительные рациональные, но не целые числа a и b, такие что числа a – b,a² – b², … ,aⁿ – bⁿ – целые.

Задача 7: Докажите, что среди 50 чисел от 1 до 100, среди которых нет двух с суммой 100, всегда найдется точный квадрат.