 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1998 | Показать решения |
|
|
| Ирландская математическая олимпиада.. 1998 |
|
|
Докажите, что если x – вещественное число не равное нулю, то
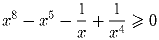
Расстояния внутренняя точка равностороннего треугольника P до трёх его вершин равно 3, 4 и 5 соответственно. Найдите площадь треугольника.
Задача 3:Докажите, что число, запись которого в десятичной системе
счисления выглядит как 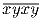 , не может быть точным кубом.
Найдите наименьшее число b > 1 такое, что в системе счисления с
основанием b найдётся точный куб вида
, не может быть точным кубом.
Найдите наименьшее число b > 1 такое, что в системе счисления с
основанием b найдётся точный куб вида 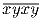 .
.
Докажите, что круг радиуса 2 может быть покрыт семью (возможно перекрывающимися) кругами радиуса 1.
Задача 5:Докажите, что если x² – x – целое число, и при некотором n ≥ 3 xn – x – целое число, то x – также целое число.
Задача 6:Найдите все натуральные числа n, у которых ровно 16 натуральных делителей 1 = d1 < d2 < … < d16 = n, d6 = 18, а d9 – d8 = 17.
Задача 7: Докажите, что для любых положительных вещественных чисел a, b и c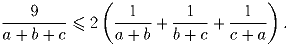
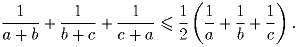
Задача 8:
a) Докажите, что множество всех натуральных чисел 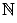 может быть представлено в виде объединения трёх попарно непересекающихся
подмножеств так, что если
может быть представлено в виде объединения трёх попарно непересекающихся
подмножеств так, что если 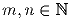 , а |m – n| = 2, или 5, то
m и n попадут в разные подмножества.
, а |m – n| = 2, или 5, то
m и n попадут в разные подмножества.
б) Докажите, что 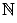 может быть представлено в виде
объединения четырёх попарно непересекающихся подмножеств так, что если
может быть представлено в виде
объединения четырёх попарно непересекающихся подмножеств так, что если
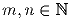 , а |m – n| = 2, 3 или 5, то m и n попадут в
разные подмножества. Докажите также, что представить
, а |m – n| = 2, 3 или 5, то m и n попадут в
разные подмножества. Докажите также, что представить 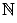 в
виде объединения трёх непересекающихся подмножеств, обладающих этим
свойством, нельзя.
в
виде объединения трёх непересекающихся подмножеств, обладающих этим
свойством, нельзя.
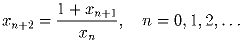
Найдите x1998.
Задача 10: В треугольнике ABC длины всех трёх сторон – натуральные числа, ∠ A = 2 ∠ B, ∠ C > 90. Найдите минимальную возможную длину периметра.
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1998 | Показать решения |