 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Корея >> 1995 >> 2 тур | Показать решения |
|
|
| Корейская математическая олимпиада.. 1995. 2 тур |
|
|
Докажите, что для любого натурального m существуют целые числа a и b такие, что
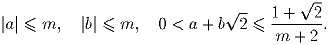
Задача 2:
Найдите все функции 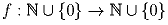 удовлетворяющие
соотношениям 2f(m² + n²) = (f(m))² + (f(n))² для всех m,n и
f(m²) ≤ f(n²) для всех m ≤ n.
удовлетворяющие
соотношениям 2f(m² + n²) = (f(m))² + (f(n))² для всех m,n и
f(m²) ≤ f(n²) для всех m ≤ n.
Задача 3:
На стороне BC равностороннего треугольника со стороной 1 выбрали точку D. r1 и r2 – радиусы окружностей вписанных в треугольники ABD и ADC. Выразите r1r2 через BD и найдите максимальное значение r1r2.
Задача 4:
O – центр окружности описанной около треугольника ABC. Из произвольной точки плоскости P опустили перпендикуляры на прямые содержащие стороны треугольника – PA1, PB1, PC1. Выразите отношение площадей треугольников ABC и A1B1C1 через радиус описанной около ABC окружности и длину отрезка OP.
Задача 5:
p = (a,b) – простое число, притом p² делит a. Докажите, что многочлен xn + 2 + axn + 1 + bxn + a + b нельзя представить в виде произведения двух многочленов с целыми коэффициентами, степени которых больше 1.
Задача 6:
Дверь закрыта на несколько замков. У каждого из m человек есть несколько ключей, притом, никакие n человек не могут открыть дверь, а любые n + 1 человек могут. Найдите наименьшее количество замков на которые закрыта дверь и определите количество ключей у каждого человека.
| Задачная база >> Национальные зарубежные олимпиады >> Корея >> 1995 >> 2 тур | Показать решения |