 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Латвия >> 1995 >> 11 класс | Показать решения |
|
|
| Латвийская математическая олимпиада.. 1995. 11 класс |
|
|
Докажите, что для любых не равных 0 чисел a1,a2, … ,c3 знаки * можно заменить на знаки < и > так, что система неравенств
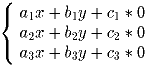
Задача 2:
Решите уравнение в натуральных числах: x(x + 1) = y7.
Задача 3:
В пространстве отмечены 4 точки не лежащие в одной плоскости. Какое количество параллелепипедов с вершинами в этих точках можно построить?
Задача 4:
На сторонах AB, BC, CD, AD выпуклого четырехугольника ABCD взяли точки M, N, P, Q соответственно так, что AM = BN = CP = DQ. Оказалось, что MNPQ – квадрат. Докажите, что ABCD тоже квадрат.
Задача 5:
Клетки квадрата n × n покрашены в несколько цветов, притом раскраски любых двух столюцов различны. Докажите, что можно выбрать одну строчку так, что после ее вычеркивания раскраски любых двух столбцов останутся различными.
| Задачная база >> Национальные зарубежные олимпиады >> Латвия >> 1995 >> 11 класс | Показать решения |