 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1992 | Показать решения |
|
|
| Испанская математическая олимпиада.. 1992 |
|
|
Натуральное число N делится нацело на 83 и количество натуральных делителей N² равно 63. Чему равно N, если известно, что это наименьшее число обладающее перечисленными выше свойствами.
Задача 2:Даны два непересекающихся круга различных радиусов. Постройте прямую, параллельную данной, такую, что сумма длин отрезков, являющихс пересечением кругов с прямой, была бы равна данному.
Задача 3:a, b, c и d неотрицательные целые числа и (a + b)² + 2a + b = (c + d)² + 2c + d. Докажите, что a = c и b = d.
Докажите, что если вместо предыдущего равенства верно: (a + b)² + 3a + b = (c + d)² + 3c + d, то также a = c и b = d.
Покажите, что существуют такие a ≠ c и b ≠ d, что (a + b)² + 4a + b = (c + d)² + 4c + d.
Задача 4:
Рассмотрим арифметическую прогрессию 3, 7, 11, 15, … Докажите, что в ней существует бесконечное количество простых чисел.
Задача 5:Дан треугольник ABC. Постройте точку P такую, что ∠ PAB = ∠ PBC = ∠ PCA. Выразите тригонометрические функции этого угла через тригонометрические функции углов A, B и C.
Задача 6:
Для натурального числа n > 0 и комплексного z = x + iy, для которого x² + y² = 1, может выполняться или нет следующее равенство:
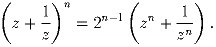
1) Найдите S(n) для n = 2, 3, 4.
2) Найдите верхнюю границу (зависящую от n) количества элементов S(n) для n > 5.
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1992 | Показать решения |