 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1995 >> 1 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1995. 1 тур |
|
|
Найдите все пары натуральных чисел (x,y) такие, что числа
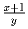 и
и 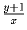 также натуральные.
также натуральные.
n – натуральное число больше 1. Решите систему уравнений:
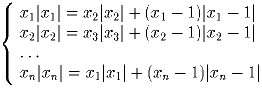
Четырехугольник со сторонами a,b,c и d вписан в окружность радиуса R. Докажите, что если a² + b² + c² + d² = 8R², то либо один из углов четырехугольника прямой, либо его диагонали перпендикулярны.
Задача 4:В некоторой школе 64 ученика приняли участие в 5 олимпиадах, в каждой из которых их приняло участие не менее 19. Никто из школьников не участвовал более чем в трех олимпиадах. Для любых трех олимпиад был по крайней мере один их общий участник. Докажите, что какие-то пять школьников приняли участие в двух олимпиадах.
Задача 5:Даны положительные числа a и b. Докажите, что следующие два утверждения эквивалентны:
(1) 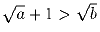 ;
;
(2) Для любого 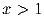
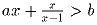 .
.
Внутри треугольника ABC выбрали точку P. Лучи AP, BP и CP пересекают стороны треугольника в точках A′, B′ и C′ соответственно. Положим
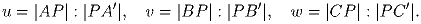
(a) Существует ли такая дифференцируемая функция, не обращающаяся в 0 на всей вещественной оси и для любого x удовлетворяющая условию 2f(f(x)) = f(x) ≥ 0?(b) Существует ли такая дифференцируемая функция, не обращающаяся в 0 на всей вещественной оси и для любого x удовлетворяющая условию – 1 ≤ 2f(f(x)) = f(x) ≤ 1?
Задача 8:Двугранный угол между боковой стороной правильной n-гранной
пирамиды (все боковые ребра равны между собой, а основание – правильный
n-угольник) и ее основанием равен α , угол между основанием и
боковым ребром – β . Докажите, что
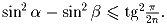
a и b – два положительных числа с суммой 1. a³ и b³ – рациональные числа. Докажите, что a и b тоже рациональные.
Задача 10:На прямой k взяли три точки и из каждой провели по два луча в одну полуплоскость относительно k, притом любые два луча пересекаются. Пара лучей с общей вершиной пересекаясь с другой парой лучей образуют выпуклый четырехугольник, таким образом получается три четырехугольника. Докажите, что если в два из них можно вписать окружность, то можно вписать окружность и в третий.
Задача 11:Из множества 1,2, … ,n выбирают m чисел (n > m > 1). Найдите ожидаемое значение разности между максимальным вытащенным числом и минимальным.
Задача 12:Дана последовательность xn:
x1 = ½, 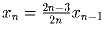 при n > 1.
Докажите, что для любого n x1 + x2 + • s + xn < 1.
при n > 1.
Докажите, что для любого n x1 + x2 + • s + xn < 1.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1995 >> 1 тур | Показать решения |