Задача 1:
Верно ли, что любое положительное рациональное число можно представить в виде
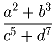
, где числа a,b,c,d – натуральные?
Задача 2:
D – точка пересечения биссектрисы угла A треугольника ABC
с его описанной окружностью. K и L – ортогональные проекции
точек B и C на прямую AD. Докажите, что AD ≥ BK + CL.
Задача 3:
В клетках доски n × n записано n² различных натуральных чисел.
В каждом столбце клетку, содержащую максимальное число покрасили в
красный цвет. На доску поставили n не бьющих друг друга ладей,
притом оказалось, что сумма чисел в клетках, на которых они стоят
максимальна (по отношению к остальным таким расстановкам).
Докажите, что по крайней мере одна ладья стоит на красной клетке.
Задача 4:
I – центр вписанной в треугольник ABC окружности.
Прямые BI и CI пересекают стороны AC и AB
в точках D и E соответственно.
Известно, что AB ≠ AC.
Найдите все возможные значения угла BAC для которых
может выполняться равенство DI = EI.
Задача 5:
Существует ли функция
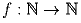
такая, что
f(f(n)) = 2n для любого n.
Задача 6:
w – квадратный трехчлен с целыми коэффициентами.
Все значения w в целых точках – квадраты целых чисел.
Докажите, что w – квадрат некоторого многочлена.


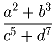 , где числа a,b,c,d – натуральные?
, где числа a,b,c,d – натуральные?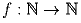 такая, что
f(f(n)) = 2n для любого n.
такая, что
f(f(n)) = 2n для любого n.