Задача 1: Найти наименьшее A, при котором для любых двух квадратов общей
площади 1 найдется такой прямоугольник площади A, в котором можно
разместить без наложения указанные квадраты. Можно считать, что
стороны квадратов параллельны сторонам прямоугольника.
Задача 2: Радиусы двух окружностей соответственно 1 и 3, расстояние между
центрами окружностей – 10. Найти геометрическое место середин
отрезков, соединяющих точки данных окружностей.
Задача 3: В школе работает 6 кружков. Каждый из 20 учеников класса может
посещать любое количество кружков – от 0 до 6. Верно ли, что
обязательно найдутся такие 5 учеников и такие 2 кружка, что все
пятеро либо посещают оба кружка, либо не посещают ни один из этих
двух кружков?
Задача 4: Пусть S – множество упорядоченных троек (a,b,c) различных
элементов конечного множества A. Выполняются следующие условия:
 ;
;
 ;
;
 .
.
Доказать, что существует такая функция
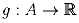
, что из
двойного неравенства g(a) < g(b) < g(c) следует: (a,b,c) ∈ S.
Задача 5: Пусть p – простое число, большее 3, k = [2p/3]. Доказать, что сумма
биномиальных коэффициентов 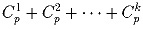 делится на
p².
делится на
p².
Задача 6: Пусть 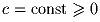 . Опишите множество всех непрерывных функций
. Опишите множество всех непрерывных функций
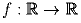 таких, что
таких, что 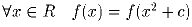 .
.


 ;
;
 ;
;
 .
.
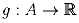 , что из
двойного неравенства g(a) < g(b) < g(c) следует: (a,b,c) ∈ S.
Задача 5:
, что из
двойного неравенства g(a) < g(b) < g(c) следует: (a,b,c) ∈ S.
Задача 5: 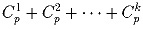 делится на
p².
делится на
p².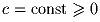 . Опишите множество всех непрерывных функций
. Опишите множество всех непрерывных функций
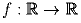 таких, что
таких, что 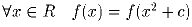 .
.