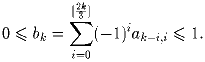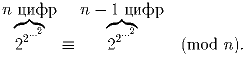Задача 1:
Пусть s(x) есть расстояние между числом x и ближайшим к нему
целым числом.
Для произвольного натурального n вычислить
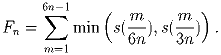
Задача 2: Пусть f — дважды дифференцируемая функция, для которой
f″(x) + f(x) = – xg(x)f′(x),
где g(x) ≥ 0 при всех x. Доказать, что функция f(x) ограничена.
Задача 3:
Для каждого натурального n запишем сумму
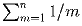
в виде α
n/ β
n, где α
n и β
n – взаимно простые числа.
Найти все n, при которых β
n не делится на 5.
Задача 4: (1 + x + x²)m. Докажите, что для всех целых
k ≥ 0
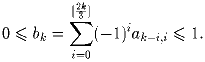
Задача 5: Докажите, что для n ≥ 2
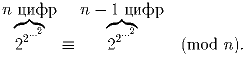
Задача 6:
Разбиение треугольника со сторонами длиной 3, 4, 5 его средними линиями на 4
части имеет диаметр
5/2.
Найти наименьший диаметр разбиения этого треугольника на 4 части.
(Диаметр разбиения – это точная верхняя грань расстояний между
точками из одной части разбиения).


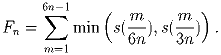
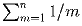 в виде α n/ β n, где α n и β n – взаимно простые числа.
Найти все n, при которых β n не делится на 5.
Задача 4:
в виде α n/ β n, где α n и β n – взаимно простые числа.
Найти все n, при которых β n не делится на 5.
Задача 4: