 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1990 | Показать решения |
|
|
| Математическая олимпиада США. 1990 |
|
|
Номера лицензий, выдаваемых каждым штатом состоят из 6 цифр (кажда от 0 до 9). Каждые два номера должны отличаться не менее чем в двух цифрах. (Таким образом номера 027592 и 020592 не могут использоватьс одновременно.) Найдите максимальное количество лицензий, которые может выдать штат.
Задача 2:Последовательность функций \,fn(x)\, определена рекуррентно:
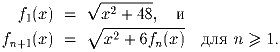
Для каждого натурального n найдите все вещественные решения уравнени \,fn(x) = 2x\,.
Задача 3:Ожерелье A составлено из 14, а ожерелье B из 19 бусин. Докажите, что для любого нечетного n ≥ 1 можно так перенумеровать все 33 бусины числами от n до n + 32, что номера любых двух соседних бусин будут взаимно просты. (Ожерелье здесь рассматривается как круг, на котором каждая бусина имеет двух соседей.)
Задача 4:Сколько существует чисел, n-ричная запись которых содержит k цифр, и каждая цифра (за исключением самой левой) отличается на ± 1, от некоторой цифры, стоящей левее нее.
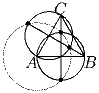
Задача 5:ABC – остроугольный треугольник. На стороне \,AB\, как на диаметре, построили окружность, которая пересекает высоту \,CC′\, и ее продолжение в точках \,M\, и \,N\,. Окружность, построенная на диаметре \,AC\, пересекает высоту \,BB′\, ее продолжение в точках \,P\, и \,Q\,. Докажите, что точки \,M,N,P,Q\, лежат на одной окружности.
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1990 | Показать решения |