 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1998 | Показать решения |
|
|
| Математическая олимпиада США. 1998 |
|
|
Множество натуральных чисел от 1 до 1998 разбили на непересекающиеся пары ai,bi так, что числа в каждой паре отличаются на 1 или 6. Докажите, что число |a1 – b1| + |a2 – b2| + … + |a999 – b999| оканчивается на цифру 9.
Задача 2:Даны две концентрические окружности. Хорда AC большей окружности касается меньшей в точке B. D – середина отрезка AB. Прямая, проходящая через точку A пересекает меньшую окружность в точках E и F, притом серединные перпендикуляры DE и CF пересекаются в точке M, лежащей на AB. Найдите отношение AM/MC.
Задача 3:
a0,a1 … ,an – числа из интервала (0, π /2), удовлетворяющие условию
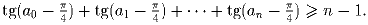 Докажите, что tg a0 tg a1 • s tg an ≥ nn + 1.
Докажите, что tg a0 tg a1 • s tg an ≥ nn + 1.
Задача 4:
Доска 98 × 98 покрашена в шахматном порядке. Разрешается в любом прямоугольнике, со сторонами параллельными сторонам квадрата поменять цвета на противоположные. Определите минимальное количество операций, необходимых для того, чтобы все клетки доски стали одного цвета.
Задача 5:Докажите, что для любого n ≥ 2 существует n-элементное множество, квадрат разности любых двух элементов, которого делит их произведение.
Задача 6:Для любого n ≥ 5 найдите максимальое k такое, что существует выпуклый n-угольник A1A2 … An для которого ровно в k четырехугольниов AiAi + 1Ai + 2Ai + 3 можно вписать окружность.
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1998 | Показать решения |