 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1980 >> Районный тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1980. Районный тур. 10 класс |
|
|
Задача 2: Доказать, что
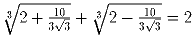
Задача 3:
Задача 4: Точка O – середина высоты правильного тетраэдра ABCD. Через точку O проведены всевозможные прямые, отрезки которых, заключенные внутри ABCD, делятся в точке O пополам. Какое множество образуют концы этих отрезков на поверхности тетраэдра?
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1980 >> Районный тур >> 10 класс | Показать решения |