 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 8 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1981. Районный тур. 8 класс |
|
|
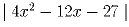 –
простое число.
–
простое число.Задача 2: a > b > 0; a² + b² = 6ab. Найти
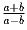 .
.Задача 3: Из точки M, взятой вне угла A, проведены к нему две секущие прямые, одна из которых отсекает на сторонах угла два равных отрезка AB и AC, а другая пересекает эти стороны в точках D и E соответственно. Доказать, что BD:CE = MD:ME.
Задача 4: xx + yy = xy + yx, x и y – натуральные числа. Докажите, что x = y.
Задача 5:
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 8 класс | Показать решения |